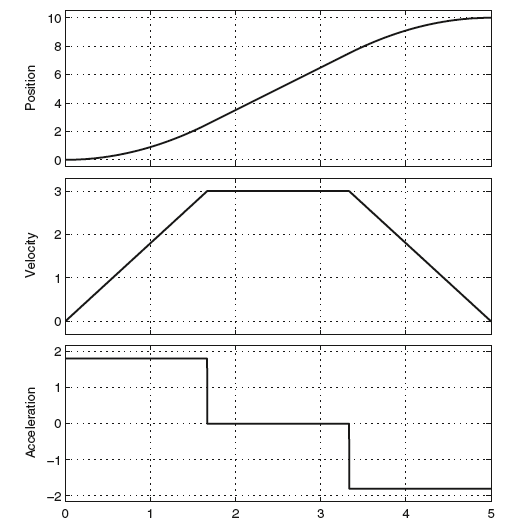
梯形速度曲线轨迹

公式

\[ \begin{aligned} q(t)&=\begin{cases} v_s+\frac{1}{2}at^2,&0\le t<t_a\\ q_a+v_c(t-t_a),&t_a\le t<t_a+t_c\\ q_a+q_c+v_c(t-t_a-t_c)+\frac{1}{2}d(t-t_a-t_c)^2,&t_a+t_c\le t<t_a+t_c+t_d \end{cases}\\ v(t)&=\begin{cases} v_s+at,&0\le t<t_a\\ v_c,&t_a\le t<t_a+t_c\\ v_c+d(t-t_a-t_c),&t_a+t_c\le t<t_a+t_c+t_d \end{cases}\\ a(t)&=\begin{cases} a,&0\le t<t_a\\ 0,&t_a\le t<t_a+t_c\\ d,&t_a+t_c\le t<t_a+t_c+t_d \end{cases}\\ \end{aligned} \]

• 加速时间: \(t_a\)
• 匀速时间: \(t_c\)
• 减速时间: \(t_d\)
• 初始速度: \(v_s\)
• 最大速度: \(v_m\)
• 终止速度: \(v_e\)
• 加速位移: \(q_a=v_st_a+\frac{1}{2}at_a^2\)
• 匀速位移: \(q_c=v_ct_c\)
• 减速位移: \(q_d=v_ct_c+\frac{1}{2}dt_d^2\)
• 总位移: \(t=t_a+t_c+t_d\)
• 总位移: \(q=q_a+q_c+q_d\)
• 匀速度: \(v_c\)
• 加速度: \(a\)
• 减速度: \(d\)

计算

假设没有匀速阶段, 只有加速阶段和减速阶段, 运动中的最大速度为​\(v\), 则有 \[ q=q_a+q_c=\frac{v^2-v_s^2}{2a}+\frac{v_e^2-v^2}{2d} \] 解得最大速度为 \[ |v|=\sqrt{\frac{av_e^2-dv_s^2-2lad}{a-d}} \]

1. 如果 \(|v|>|v_m|\), 则存在匀速阶段.

   \[ \begin{cases} t_a=\cfrac{v_m-v_s}{a}\\ t_c=\cfrac{q-q_a-q_d}{v_c}\\ t_d=\cfrac{v_e-v_m}{d}\\ \end{cases} \]

2. 否则没有匀速阶段.

   1. 如果 \(|v_s|<|v|\le|v_e|\), 只有加速阶段.

   \[ |v_e|=\sqrt{v_s^2+2la} \] \[ \begin{cases} t_a=\cfrac{v_e-v_s}{a}\\ t_c=0\\ t_d=0\\ \end{cases} \]

   2. 如果 \(|v_s|\ge|v|>|v_e|\), 只有减速阶段.

   \[ |v_e|=\sqrt{v_s^2+2ld} \] \[ \begin{cases} t_a=0\\ t_c=0\\ t_d=\cfrac{v_e-v_s}{d}\\ \end{cases} \]

   3. 如果 \(|v|>|v_s|\), \(|v|>|v_e|\), 则存在加速阶段和减速阶段.

   \[ \begin{cases} t_a=\cfrac{v-v_s}{a}\\ t_c=0\\ t_d=\cfrac{v_e-v}{d}\\ \end{cases} \]

3. 最后利用公式计算位移和速度.

实现

https://github.com/tqfx/liba/blob/tqfx/src/traptraj.c