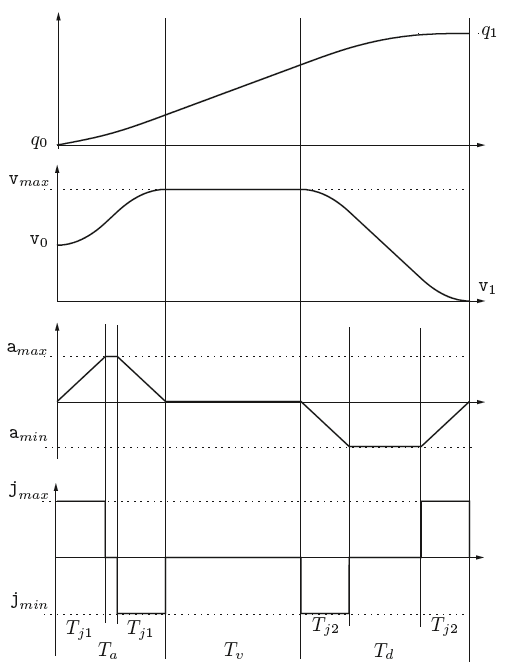
钟形速度曲线轨迹

公式

\[ \begin{aligned} p(t)&=\begin{cases} p_0+v_0t+j_m\cfrac{t^3}{6},&t\in[0,T_{aj}]\\ p_0+v_0t+\cfrac{a_m}{6}(3t^3-3tT_{aj}+T_{aj}^2),&t\in[T_{aj},T_a-T_{aj}]\\ p_0+(v_m+v_0)\cfrac{T_a}{2}-v_m(T_a-t)+j_m\cfrac{(T_a-t)^3}{6},&t\in[T_a-T_{aj},T_a]\\ p_0+(v_m+v_0)\cfrac{T_a}{2}+v_m(t-T_a),&t\in[T_a,T_a+T_v]\\ p_1-(v_m+v_1)\cfrac{T_d}{2}+v_m(t-T+T_d)-j_m\cfrac{(t-T+T_d)^3}{6},&t\in[T-T_d,T-T_d+T_{dj}]\\ p_1-(v_m+v_1)\cfrac{T_d}{2}+v_m(t-T+T_d)\\\quad+\cfrac{d_m}{6}\left(3(t-T+T_d)^2-3(t-T+T_d)T_{dj}+T_{dj}^2\right),&t\in[T-T_d+T_{dj},T-T_{dj}]\\ p_1-v_1(T-t)-j_m\cfrac{(T-t)^3}{6},&t\in[T-T_{dj},T] \end{cases}\\ \dot(p)(t)&=\begin{cases} v_0+j_m\frac{t^2}{2},&t\in[0,T_{aj}]\\ v_0+a_m(t-\cfrac{T_{aj}}{2}),&t\in[T_{aj},T_a-T_{aj}]\\ v_m-j_m\cfrac{(T_a-t)^2}{2},&t\in[T_a-T_{aj},T_a]\\ v_m,&t\in[T_a,T_a+T_v]\\ v_m-j_m\cfrac{(t-T+T_d)^2}{2},&t\in[T-T_d,T-T_d+T_{dj}]\\ v_m+d_m(t-T+T_d-\cfrac{T_{dj}}{2}),&t\in[T-T_d+T_{dj},T-T_{dj}]\\ v_1+j_m\cfrac{(T-t)^2}{2},&t\in[T-T_{dj},T] \end{cases}\\ \ddot(p)(t)&=\begin{cases} j_mt,&t\in[0,T_{aj}]\\ j_mT_{aj}=a_m,&t\in[T_{aj},T_a-T_{aj}]\\ j_m(T_a-t),&t\in[T_a-T_{aj},T_a]\\ 0,&t\in[T_a,T_a+T_v]\\ -j_m(t-T+T_d),&t\in[T-T_d,T-T_d+T_{dj}]\\ -j_mT_{dj}=d_m,&t\in[T-T_d+T_{dj},T-T_{dj}]\\ -j_m(T-t),&t\in[T-T_{dj},T] \end{cases}\\ p^{(3)}(t)&=\begin{cases} j_m,&t\in[0,T_{aj}]\\ 0,&t\in[T_{aj},T_a-T_{aj}]\\ -j_m,&t\in[T_a-T_{aj},T_a]\\ 0,&t\in[T_a,T_a+T_v]\\ -j_m,&t\in[T-T_d,T-T_d+T_{dj}]\\ 0,&t\in[T-T_d+T_{dj},T-T_{dj}]\\ j_m,&t\in[T-T_{dj},T] \end{cases} \end{aligned} \]

计算

0. 如果 \(p_0>p_1\), 则

\[ \begin{aligned} p_0&=-p_0\\ p_1&=-p_1\\ v_0&=-v_0\\ v_1&=-v_1\\ \end{aligned} \]

1. 如果 \((v_m-v_0)j_m<a_m^2\), 达不到最大加速度, 则

   \[ \begin{aligned} T_{aj}&=\sqrt{\frac{v_m-v_0}{j_m}}\\ T_a&=2T_{aj}\\ a_m&=+j_mT_{aj} \end{aligned} \] 否则 \[ \begin{aligned} T_{aj}&=\frac{a_m}{j_m}\\ T_a&=T_{aj}+\frac{v_m-v_0}{a_m}\\ a_m&=+a_m \end{aligned} \]

2. 如果 \((v_m-v_1)j_m<a_m^2\), 达不到最大减速度, 则

   \[ \begin{aligned} T_{dj}&=\sqrt{\frac{v_m-v_1}{j_m}}\\ T_d&=2T_{dj}\\ d_m&=-j_mT_{dj} \end{aligned} \] 否则 \[ \begin{aligned} T_{dj}&=\frac{a_m}{j_m}\\ T_d&=T_{dj}+\frac{v_m-v_1}{a_m}\\ d_m&=-a_m \end{aligned} \]

3. 计算匀速阶段时间 \[ T_v=\frac{p_1-p_0}{v_m} -\frac{T_a}{2}\left(1+\frac{v_0}{v_m}\right) -\frac{T_d}{2}\left(1+\frac{v_1}{v_m}\right) \] 如果 \(T_v>0\), 则存在匀速阶段，时间计算结束.

4. 如果 \(T_v<=0\), 则 \(T_v=0\). \[ \begin{aligned} T_{aj}&=T_{dj}=T_{j}=\frac{a_m}{j_m}\\ T_a&=\cfrac{\frac{a_m^2}{j_m}+\sqrt\Delta-2v_0}{2a_m}\\ T_d&=\cfrac{\frac{a_m^2}{j_m}+\sqrt\Delta-2v_1}{2a_m}\\ \Delta&=\frac{a_m^4}{j_m^2}+2(v_0^2+v_1^2)+a_m\left(4(p_1-p_0)-2\frac{a_m}{j_m}(v_0+v_1)\right) \end{aligned} \]

   1. 如果 \(T_a<0\), 只有减速阶段, 则 \(T_a=0\),\(T_{aj}=0\), \[ \begin{aligned} T_d&=2\cfrac{p_1-p_0}{v_1+v_0}\\ T_{dj}&=\frac{j_m(p_1-p_0)-\sqrt{j_m(j_m(p_1-p_0)^2+(v_1-v_0)(v_1+v_0)^2)}}{j_m(v_1+v_0)} \end{aligned} \]

   2. 如果 \(T_d<0\), 只有加速阶段, 则 \(T_d=0\),\(T_{dj}=0\), \[ \begin{aligned} T_a&=2\cfrac{p_1-p_0}{v_1+v_0}\\ T_{aj}&=\frac{j_m(p_1-p_0)-\sqrt{j_m(j_m(p_1-p_0)^2+(v_0-v_1)(v_1+v_0)^2)}}{j_m(v_1+v_0)} \end{aligned} \]

   3. 如果 \(T_a\ge2T_j\), \(T_d\ge2T_j\), 则 \[ \begin{aligned} a_m&=+j_mT_{aj}\\ d_m&=-j_mT_{dj}\\ v_m&=v_0+(T_a-T_{aj})a_m=v_1-(T_d-T_{dj})d_m \end{aligned} \]

   4. 如果以上条件都不满足并且 \(a_m>\epsilon\), 则令 \(a_m=\alpha a_m,0<\alpha<1\), 然后重复步骤 4.

5. 最后利用公式计算位置、速度和加速度.

实现

https://github.com/tqfx/liba/blob/main/src/trajbell.c